Determination of the Interaction Potential of Microspheres in a Plasma

by U. Konopka

Since nearly all plasmas in space and in the laboratory are dusty plasmas, the interaction between dust and plasma is of fundamental interest. Especially the plasma influence on the interaction between the particles themselves is of high importance, because it affects for instance the effectivity of coagulation processes and, as in the laboratory plasmas, explains the behavior of plasma-crystal structures which have been studied in recent years.

Thus, first experiments have been performed to determine the interaction of microspheres for the special conditions that are typical for plasma-crystal experiments. These collision experiments with micrometer-sized particles in the sheath of a radio-frequency discharge show, that the two-particle-interaction potential parallel to the plasma-sheath boundary coincides with a Yukawa potential. It is demonstrated, that the investigations of colliding particles are in general an appropriate method to obtain the interaction potential. In addition collisions of microspheres open up a new possibility to study the structure of plasma sheaths with comparatively small distortions.

Dust particles that are embedded into a plasma environment are permanently bombarded by electrons, ions and neutral gas particles. Hence each particle charges up until the influence of its surface potential leads to an equilibrium between the electron and ion current to its surface. The net charge on the particles in the performed experiments is negative, since here the electrons have a higher mobility than the ions. The interactions with neutral gas particles result mainly in damping of the particle movement as it is decribed by the Epstein law (collisional friction).

The surface potential of a particle in a plasma is screened by a charge redistribution in its local neighbourhood. Therefore the inter-particle force decreases rapidly with increasing distance. In the case of Boltzmann-distributed electrons and ions this screening phenomenon has been solved analytically. A linearised Ansatz leads to the well-known Yukawa potential, where the charges of the particles have to be replaced by effective charge values. For more general conditions, as they occur for example in laboratory plasma-crystal experiments, we cannot expect to have simple Boltzmann distributions. In this special case, where small plastic spheres are levitated in a plasma sheath, it is well known that the ions have a strong vertical anisotropic velocity distribution due to acceleration in the electric field in the sheath. Because of the magnitude of this vertical velocity the ions cannot contribute directly to the horizontal screening of the charge of the dust particles. On the other hand, this directed ion current is slightly deviated by the particle potentials with the result of an increase in positive space-charge densities below the particles (‘ion focus effect’ – see Fig. 3.13 a). Together with the dust charges this leads to an additional dipole interaction between neighboured particles. Other effects, for instance a charge depletion of the dust particles and screening of neutral currents due to the presence of additional neighbour particles (see Fig. 3.13 b), intensifies the problem to determine the interaction potential from theory considerations alone, which makes experimental data mandatory.

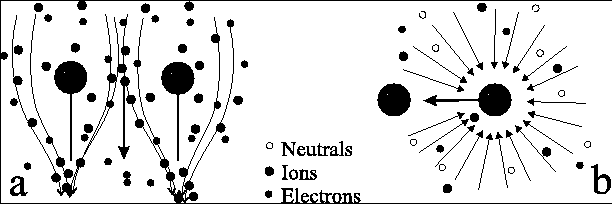
Fig. 3.13: Sketch of the so called "ion-focus effect" (a). The streaming ions are influenced by the net charge on the particles´ surface. The change of the ion trajectories leads to an increased positive space charge below the microspheres. Thus, an additional dipole interaction occurs between neighboured particles.In addition a shielding of the permanent neutral flux due to the cross section of a neighbour particle (b) influences the inter-particle potential.

Two types of experiments have been performed here at the institute in collaboration with the institute of space simulation from the DLR with the aim to measure the two-particle interaction. First, the horizontal oscillation of a single particle within a confinement potential in an radio-frequency plasma sheath is investigated to obtain the details of this confinement. Second, the trajectories of two in the same confinement in the plasma sheath centrally colliding identical microspheres are analyzed. This give us the possibility to determine directly the two-particle interaction-potential by experiment without knowing the plasma parameters. In addition, practically as a side effect, we obtain the confining potential that holds the particles in their equilibrium position and also a value for the friction forces acting on them.

The experiments were carried out in the same vacuum chamber that is used for the plasma-crystal experiments. Depending on the experiment objective, one or two micrometer-sized particles are injected into the plasma in contrast to the plasma crystal experiments where many microspheres are needed. The particles are confined in the center of the chamber by the electric potential of a copper ring that is placed on one of the radio-frequency electrodes and which produces a "trap" (experimental setup see Fig. 3.14). 

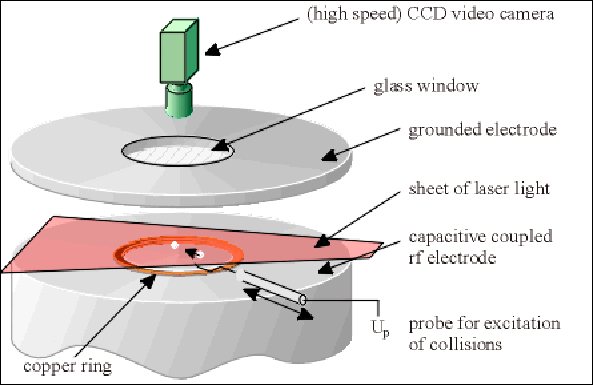
Fig. 3.14: Sketch of the experimental setup.

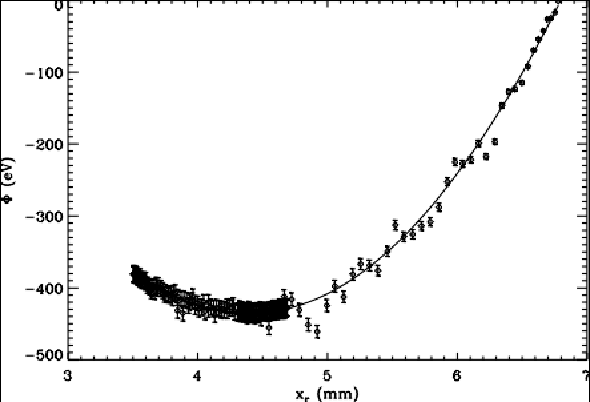
Fig. 3.15: A single-particle oscillation around its equilibrium position allows the determination of the displayed potential as function of the absolute position. In addition a value for the friction force can be estimated. The measured potential is consistent with a parabola potential as given by the solid line. The obtained friction constant is within a 20 % range to the estimated Epstein-drag constant.

With the help of an appropriate manipulation device, which consists of a modified Langmuir probe, the particles can be moved horizontally within the sheath. In particular a single particle can be removed from the central region and then set free in its movement again at a different location. Because of the confining potential the particle is accelerated back towards the center. Here it collides with a second particle or, in the case of a single-particle experiment, executes a damped oscillation in the confinement potential. The latter is used to measure the details of the confinement (see Fig. 3.15) and to estimate a value for the friction constant assuming that the friction force is proportional to the particle velocity. To do this the equation of motion for a single particle in an arbitrary conservative confinement potential, that is assumed to depend on particle separation only, is integrated taking a friction force into account. The potential can then be calculated directly from the particle trajectory and its derived velocity except for a numerical constant offset. (In practice, the calculation is somewhat more involved, as the parameter for the friction has to be iterated until the calculated potential is continuous in its spatial dependency.)

The one-particle experiments show that the determined confinement is in good agreement with a parabolic potential. We can therefore assume that a single particle, as well as the center of mass for a two-particle system, will perform a damped harmonic oscillation. This can in turn be used in the measurement of the inter-particle potential by estimating the parabola constant of the confining potential, as well as the friction constant, from a fit of the center-of-mass trajectory of the two colliding particles with a damped harmonic oscillation. The inter-particle potential along the collision axis itself can then be calculated in a similar manner to the confinement measurement, using the relative trajectory of the collision partners. The measurements show a good agreement with a Yukawa potential (see. Fig. 3.16). Consequently it is obvious to quantify an effective particle charge and a screening length from the obtained interaction potential.

Fig. 3.16: The interaction potential, as determined from typical experimental data, shows a good agreement with a Yukawa potential (solid line).

Fig. 3.17: Simulated relative trajectory of a two-particle collision with a Yukawa-type interaction for the experimentally given boundary conditions and the determined values for effective charge, screening length, parabola and friction constant. The experimentally determined distances (diamonds) are overlaid on the simulated ones (solid line).

To confirm the derived results, extensive computer simulations were performed. A two-particle collision simulation with the same boundary conditions as in the experiments (i.e. starting velocities, start positions) together with the previously experimentally determined parameters for friction, confinement, effective charge and screening length shows a very close match to the experimental data (see Fig. 3.17).

Since the levitation height strongly depends on the dust-particle radius and therefore probe measurements of the acting potentials can be performed for different heights, the two-particle collisions as well as the one-particle oscillations can be used also to obtain a better understanding of the physical processes occurring over a large range in a plasma sheath.