Deutsch

PKE Nefedov More Results (3)

Forces and potential energy inside the void

A complex plasma is, under certain conditions, expected to build up a regular 3-D structure, a 'plasma crystal', that fills the whole volume of the plasma in microgravity. But most experiments with PKE-Nefedov aboard the ISS showed an inhomogeneous filling of the plasma discharge space. The micro-particles are located around a particle-free zone in the center, the so-called 'void'.

Often the void reaches a size half of the diameter of the whole discharge. This unexpected feature that prevents large undisturbed plasma crystals needs further investigation, also to learn more about the forces inside the plasma.

In one dedicated experiment the plasma crystal was disturbed by a gas puff and particles were placed inside the void where they were expelled immediately. (See image on the right side.) From 198 trajectories (marked in the image) we can derive the effective potential acting on the particles inside the void.

See the original data movie: AVI (4.4 MB).

First observation: After the puff the void swings back and forth. But if we take into account this motion we get distorted trajectories! The particles move in the reference frame of the plasma chamber. This means the feature that causes the void is independent from the particle cloud. It acts with reference to the plasma chamber.

From the particle trajectories we can derive the velocity of the particles. If we plot the x (=horizontal) and y velocity components separately depending on their x and y position we get the following graphs:

The x and y components of the velocities are proportional to the x and y position of the particles and can be well fitted by straight lines. The slopes of the lines gives us the spatial accelerations a_x = 0.308 s^-1 horizontally and a_y = 0.711 s^-1 vertically. These relations will be useful in the following way: Let's start with the equation of motion of a particle inside the plasma (left panel, top):

where m is the particle mass, R the gas friction coefficient and Phi the potential at the position x_i (=x,y). We get, after integration and substituting x_i' with the relation v_i(x_i) = a_i x_i found above, the equation at the bottom of the left panel.

With the experimental parameters m = 3.1x10^-14 kg and R = 1.18x10^-11 kg/s (Epstein-Drag of particles with d = 3.4 µm in Argon at p = 97 Pa) (right panel) and choosing Phi₀ = 0 we get the separated components of the effective potential:

Phi_x(x) = -1.14x10⁷ eV/m² x²   and   Phi_y(y) = -2.36x10⁷ eV/m² y²

which is clearly a parabolic dependency of the potential energy of the particles on their distance from the center. If we plot these parabolas within the limits of the void boundary in each component (see left plot below) we find the potential energy to be in the same range. This implies the void boundary is a equi-potential line (or surface in 3-D).

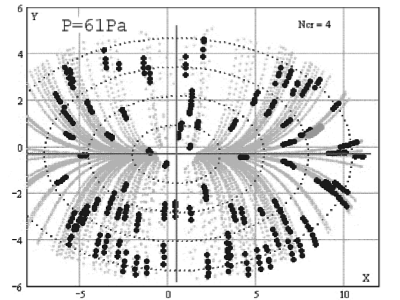
The image above, right side, shows a simulation of the particle trajectories under the assumption that the force acting on the particles inside the void increases linearly with respect to the center. The resulting parabolas fit very well the measured positions of the trajectories (black dots). This implies that the force responsible for the void formation can be assumed to be the drag force of the ions produced in the center of the discharge streaming out towards the electrodes.
Another example of the necessity of microgravity experiments, since on earth the ion drag force is covered by the force of gravity which exceeds the ion drag by an order of a magnitude.

Conclusions:

By placing particles inside the - usually particle-free - void and analysing the trajectories we gain valuable information about the conditions inside the void.

• The structure of the void is independent from the presence or distribution of the particles;
• The effective potential that drives the particles out of the void is, within measurement accuracy, of parabolic shape;
• The void boundary forms, in this experiment, an equi-potential surface;
• Experiments on parabolic flights show similar results at different parameters;
• Simulations assuming a linear central force show good agreement;
• This suggests that the ion drag force is responsible for void formation;
• Microgravity is needed in this case to see the effect of the ion drag;
• More void experiments are planned on the ISS at different parameter settings to quantify the effect;

Publication: M. Kretschmer, et al., IEEE Trans. Plasma Science, Vol. 39, No. 11, 2758 (2011)


Next: PKE-Nefedov Concluding Report

---

Updated: 2012-02-06
Contact: Michael Kretschmer