English

PKE Nefedov Mehr Ergebnisse (3)

Kraftverteilung und potentielle Energie im Void

Bei geeigneten Bedingungen sollte ein komplexes Plasma unter Schwerelosigkeit eigentlich eine regelmäßige Struktur bilden, einen Plasmakristall, der das ganze Plasmavolumen einnimmt. Doch zeigte sich, dass bei den meisten Experimenten ein ausgedehnter Bereich in der Mitte der Entladung frei von Mikropartikeln blieb. Um dieses sog. 'Void' herum sammeln sich die Partikel unter Schwerelosigkeit an.

Oftmals erreicht dieses Void mehr als den halben Durchmesser des gesamten Plasmas. Dieses überraschende Phänomen, das große, ausgedehnte Plasmakristalle verhindert, sollte zum Verständnis und zur Verbesserung der Plasmakristall-Experimente näher untersucht werden.

In einem gezielten Experiment wurde der Plasmakristall mit dem Void in der Mitte durch einen Gasstoß von der Seite zu lateralen Schwingungen angeregt. Dadurch gelangten Teilchen in das Void, aus dem sie jedoch sofort wieder hinausgetrieben wurden (siehe Bild auf der rechten Seite). Aus den Bahnen von 198 Teilchen (im Bild markiert) können wir Rückschlüsse über die Kräfte und die potentielle Energie im Void ziehen.

Original Filmdaten: AVI (4.4 MB).

Erste Beobachtung: Nach dem Stoß schwingt das Void hin und her. Wenn wir die Trajektorien der Teilchen im Bezugssystem des Voids betrachten, bekommen wir verzerrte Bahnen! Die Teilchen bewegen sich im Void also im Bezugssystem der Plasmakammer. Das bedeutet, dass das Void unabhängig von der Teilchenwolke existiert und eine Struktur innerhalb der Plasmakammer darstellt.

Von den Teilchenbahnen erhalten wir die Geschwindigkeiten der Mikroteilchen. Wenn wir diese, getrennt nach x- (=horizontal) und y-Komponente gegen ihre Position in x und y auftragen, bekommen wir folgende Bilder:

Die x- und die y-Komponenten der Geschwindigkeiten sind proportional zur jeweiligen x- und y-Position der Teilchen und können somit gut durch eine Gerade angepasst werden! Die Steigung der jeweiligen Geraden gibt uns die räumliche Beschleunigung der Teilchen a_x = 0.308 s^-1 (horizontal) und a_y = 0.711 s^-1 (vertikal). Diese Beziehung nützt uns in folgender Weise: Beginnen wir mit der Bewegungsgleichung der Partikel im Plasma (linke Tafel):

m ist die Masse der Mikroteilchen, R der Gasreibungs-Koeffizient und Phi die potentielle Energie an der jeweiligen Stelle der Teilchen x_i (=x,y). Nach der Integration der Bewegungsgleichung und dem Ersetzen von x_i' durch die oben gewonnene Beziehung v_i(x_i) = a_i x_i erhalten wir die Gleichung unten in der linken Tafel.

Mit den Experiment-Parametern m = 3.1x10^-14 kg und R = 1.18x10^-11 kg/s (Epstein-Reibung eines Teilchens mit d = 3.4 µm in Argon bei p = 97 Pa) (rechte Tafel) und der Wahl Phi₀ = 0 bekommen wir die Komponenten der potentiellen Energie:

Phi_x(x) = -1.14x10⁷ eV/m² x²   und   Phi_y(y) = -2.36x10⁷ eV/m² y²

Dies ergibt eine parabolische Abhängigkeit der potentiellen Energie vom Abstand der Teilchen vom Zentrum. Wenn wir diese Parabeln in den räumlichen Abmessungen des Voids aufzeichnen (siehe Bild links unten), sehen wir, dass am Rand des Void in beiden Richtungen die gleiche potentielle Energie vorliegt. Das deutet darauf hin, dass der Rand des Voids eine Äquipotentiallinie (oder -fläche in 3D) darstellt.

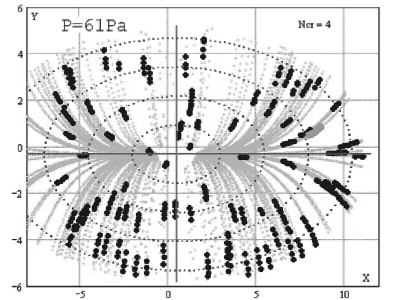
Das Bild rechts zeigt eine Simulation der Partikeltrajektorien unter der Annahme, dass die Kraft, die im Void auf die Teilchen wirkt, linear mit dem Abstand zum Zentrum zunimmt. Die sich ergebenden Parabeln passen sehr gut zu den gemessenen Teilchenpositionen (schwarze Punkte). Dies deutet darauf hin, dass die Kraft, die für das Vorhandensein des Voids hauptsächlich verantwortlich ist, die Reibungskraft der Ionen ist, die von der Mitte des Plasmas Richtung Elektroden strömen.
Dies ist auch ein Beispiel für die Notwendigkeit von Experimenten unter Schwerelosigkeit, da auf der Erde die Ionenreibung von der um Größenordnungen stärkeren Gewichtskraft der Teilchen überdeckt wird.

Zusammenfassung:

Sofern es gelingt, Mikropartikel in das ansonsten teilchenfreie Void einzubringen, erhalten wir aus den Bahnen der Teilchen Informationen über die Bedingungen im Void.

• Die Struktur des Voids ist unabhängig vom Vorhandensein und der Verteilung der Mikropartikel.
• Das effektive Potential, das die Partikel aus dem Void vertreibt, ist (im Rahmen der Messgenauigkeit) von parabolischer Form.
• In diesem Experiment stellt der Rand des Voids eine Äquipotentialfläche dar.
• Experimente auf Parabelflügen zeigen ähnliche Ergebnisse bei unterschiedlichen Parametern.
• Simulationen der Teilchenbahnen zeigen, unter der Annahme einer linearen, zentralen Kraft, sehr gute Übereinstimmungen.
• Dies deutet darauf hin, dass die Ionenreibungskraft für die Bildung des Voids verantwortlich ist.
• Schwerelosigkeit ist notwendig, um diesen Effekt der (schwachen) Ionenreibung zu sehen.
• Mehr Void-Experimente mit unterschiedlichen Experiment-Parametern sind zur Quantifizierung des Effekts auf der ISS geplant.

Publikation: M. Kretschmer, et al., IEEE Trans. Plasma Science, Vol. 39, No. 11, 2758 (2011)


Weiter: PKE-Nefedov Abschlussbericht

---

Letzte Änderung: 2012-02-06
Ansprechpartner: Michael Kretschmer